Derivation Notes on SPheRIO implementation of Back to Back Correlation
Derivation Notes on SPheRIO implementation of Back to Back Correlation
Last updated: May 15 2013
Two-particle correlation
The definition of two-particle correlation reads
- <math>\begin{align}
R(p_1,p_2) \equiv \frac{\langle N\rangle^2}{\langle N(N-1)\rangle}\frac{P_2(p_1,p_2)}{P_1(p_1)P_1(p_2)} =\frac{\langle N\rangle^2\sigma_T}{\langle N(N-1)\rangle}\frac{d^6\sigma/d^3p_1d^3p_2}{(d^3\sigma/d^3 p_1)(d^3\sigma/d^3 p_2)} \end{align}</math>
where <math>P_n</math> are the inclusive n-particle distribution function. The expression can be written down in terms of differential cross section and <math>\sigma</math>, the latter is normalized to the total cross section <math>\sigma_T</math> by the following relations
- <math>\begin{align}
&\int d^3p_1d^3p_2 (d^6\sigma/d^3p_1d^3p_2) = \langle N(N-1)\rangle\sigma_T \\ &\int d^3p (d^3\sigma/d^3 p) = \langle N\rangle\sigma_T \end{align}</math>
Note that
- <math>\begin{align}
\int d^3p (d^3\sigma/d^3 p) = \int d\Omega p^2dp \frac{d^3\sigma}{p^2dpd\Omega}= \int d\Omega \frac{d\sigma}{d\Omega} \end{align}</math>
The factor <math>\langle N\rangle</math> and <math>\langle N(N-1)\rangle</math> to r.h.s of the above expressions are due to the fact that the collision is not elastic, therefore the out-coming count is normalized to <math>\langle N\rangle</math> and <math>\langle N(N-1)\rangle</math> instead of <math>1</math>. The difference between <math>\langle N\rangle^2</math> and <math>\langle N(N-1)\rangle</math> can be ignored in big multiplicity, as in the case of nuclear collisions.
For simplicity, we first consider a state <math>|\phi\rangle</math> at zero temperature. The number of particle with momentum <math>p</math> can be obtained by calculating the expectation value of the number operator
- <math>\begin{align}
&P_1(p) = \langle\phi|\hat{n}_p|\phi\rangle \\ &\hat{n}_p=\hat{a_p}^+\hat{a_p} \end{align}</math>
in quantum mechanics. This average number is also obtained by explicitly enumerating all the possible states where at least one particle of given momentum is observed and the probability to find such a state. To calculate this we evaluate the squared modulus of the probability amplitude to transit to any state <math>X</math> after annihilation of one particle (If the corresponding transition amplitude to <math>X</math> is zero, it gives no contribution), and the corresponding number of particles is taken into account by the property of annihilation operator.
- <math>P_1(p) = \sum_X |\langle X|\hat{a_p}|\phi\rangle|^2 =\langle\phi |\hat{a_p}^+\hat{a_p}|\phi\rangle</math>
The above expression is consistent with our previous result.
One needs to take more care when considering two-particle distribution function. If the two momenta <math>p_1, p_2</math> are different, one uses <math>\hat{n}_{p_1}\hat{n}_{p_2}</math>.
- <math>\begin{align}
P_2(p_1,p_2)=\langle\phi|\hat{n}_{p_1}\hat{n}_{p_2}|\phi\rangle \end{align}</math>
But if we are to detect two particles of the same momentum, one should use <math>\hat{n}_{p_1}(\hat{n}_{p_1}-1)</math>.
- <math>\begin{align}
P_2(p_1,p_2)=\langle\phi|\hat{n}_{p_1}(\hat{n}_{p_1}-1)|\phi\rangle \end{align}</math>
This is because the number of pairs changes in the second case. The issue is automatically taken care of when one uses the second approach for Boson, for Fermi, one will never detect two particles of the same state
- <math>\begin{align}
P_2(p_1,p_2) =\sum_X |\langle X|a_{p_1}a_{p_2}|\phi\rangle|^2 =\langle\phi|a_{p_2}^+a_{p_1}^+a_{p_1}a_{p_2}|\phi\rangle \end{align}</math>
Let us consider the following state of a non-interacting system
- <math>\begin{align}
\phi\rangle = \mathcal{C}\prod_p (\hat{a_p}^+)^{N_p} \end{align}</math>
where <math>\mathcal{C}</math> is the normalization constant. Using the explicit form of <math>|\phi\rangle</math>, one obtains trivially
- <math>\begin{align}
R(p_1,p_2)=1 \end{align}</math>
Harons are emitted in collisions through interactions. To take into account the physics, these interactions have to be treated, to say the least, as external classical sources. Analytic solutions are found in a few of these models, therefore in such cases one may move on straightforward and discuss the two-particle correlations. One typical example was studied by Gyulassy et. al., surprisingly enough, the coherent state of spinless Bosons produced by a classical souce does not exibit any non-trivial two particle correlation. And non-trivial corerlatin only appreas when one imposes explicit charge conservation, or introduces some source variations (for instance, different hadrons may be emitted from independent sources). It is therefore understood that Boson statistics alone does not describe all the physics behind HBT correlation (see PRC20, 2267, (1979) for details). In general, one usually has to adopt the perturbative approach by using the Wick theorem discussed below.
Wick theorem
As shown above, two particle correlation involves terms like
- <math>\begin{align}
P_2(p_1,p_2)=\langle | a^+_{p_1}a^+_{p_2}a_{p_2}a_{p_1} |\rangle=\text{Tr}(\hat{\rho} a^+_{p_1}a^+_{p_2}a_{p_2}a_{p_1}) \end{align}</math>
In this section, we will discuss the Wick theorem and show that these term can be written in terms of two-point Green functions, then later on we will further express the resulting expression in terms of hydrodynamical variables.
For two operators <math>A, B</math>, one has
- <math>\begin{align}
&A=A^++A^- \\ &B=B^++B^- \\ &A^\bullet B^\bullet \equiv AB-\text{N}(AB)=[A^+,B^-]_{\pm} \end{align}</math>
where for instance <math>A^+</math> is proportional to annihilation operator <math>a_p</math> and it contains an integral in momentum <math>p</math> with time <math>t</math> as a parameter. The <math>-</math> applies in the case of two fermion fields, while <math>+</math> in all other cases.
As a result, the term <math>[A^+,B^-]_{\pm}</math> on the r.h.s. is a number, so it can be replaced by its vacuum expectation value
- <math>\begin{align}
\langle 0|[A^+,B^-]_{\pm}|0\rangle=\langle 0|AB|0\rangle \end{align}</math>
Therefore
- <math>\begin{align}
AB=\text{N}(AB)+\langle 0|AB|0\rangle \end{align}</math>
One then considers different time orders to obtain
- <math>\begin{align}
\text{T}\{AB\}=\text{N}(AB)+\langle 0|\text{T}\{AB\}|0\rangle \end{align}</math>
This is simply because
- <math>\begin{align}
&\text{T}\{AB\}=\pm \text{T}\{BA\}\\ &\text{N}(AB)=\pm \text{N}(BA) \end{align}</math>
This result can be generalize to N-point case to obtain the Wick theorem at zero temperature. See F.Mandl (6.30) for more details.
For finite temperature, the situation is more complicated. Although, instead of replacing the term <math>[A^+,B^-]_{\pm}</math> with its expectation value on vacuum state <math>|0\rangle</math>, one may consider the vacuum state in finite temperature, namely, <math>|\rangle</math>.
- <math>\begin{align}
A^\bullet B^\bullet = \langle |[A^+,B^-]_{\pm}|\rangle\ne\langle |AB|\rangle \end{align}</math>
But this does not help further with the evaluation, since generally
- <math>\begin{align}
\langle |\text{N}(AB)|\rangle \ne 0 \end{align}</math>
So in general one has to redefine either the split of positive and negative wave function operator or the normal order. A careful study takes a different approach and gives the Wick theorem at finite temperature, for 4-point Green function it reads
- <math>\begin{align}
\langle |a^+_{p_1}a^+_{p_2}a_{p_2}a_{p_1}|\rangle = \langle |a^+_{p_1}a_{p_1}|\rangle\langle |a^+_{p_2}a_{p_2}|\rangle +\langle |a^+_{p_1}a_{p_2}|\rangle\langle |a^+_{p_2}a_{p_1}|\rangle +\langle |a^+_{p_1}a^+_{p_2}|\rangle\langle |a_{p_2}a_{p_1}|\rangle \end{align}</math>
which does not explicitly involves normal order neither time order. In fact, the normal order (not the time order, which is defined as at zero temperature) can be employed to facilitate the proof. In particular, one can conveniently split an operator <math>A</math> in such a way, that the expectation value of normal order on thermal vacuum states is always zero (therefore <math>A^\bullet B^\bullet</math> changes accordingly). One then employs the Wick theorem at zero temperature and evaluate the expectation value of both side of the equality in thermal vacuum state, the l.h.s is defined as N-point Green function at finite temperature, while the r.h.s. is expressed in terms of two point Green functions. Therefore the above expression is obtained. See arXiv: hep-ph/9601268 for details.
HBT correlation
In the case of hydrodynamics, it is more natural to try to express physical quantities in terms of particle distribution functions. The one-particle and two-particle distributions then can be expressed as integrals on the freeze-out surface.
We will first discuss the simplest case. In free space, one-particle distribution function can be intuitively obtained as the following
- <math>\begin{align}
I(0,p_1)\equiv {p_1^0}\frac{d^3N}{d^3{p}_1}={p_1^0}\langle |a^+_{p_1}a_{p_1} |\rangle = {p_1^0} \text{Tr}(\hat{\rho} a^+_{p_1}a_{p_1}) \end{align}</math>
Note that the appearance of the factor <math>p_1^0</math> is due to dimensional arguments. Owing to the commutation relation of <math>{a_p}, {a_{p'}}</math>, <math>\langle | a^+_{p_1}a_{p_1} |\rangle</math> has the dimension of <math>[\delta(\vec p)]=[p^0]=[\text{Energy}]</math>, where one makes use of the fact that <math>\int\delta(\vec p)d^3p=1</math> and <math>d^3p/p^0</math> is invariant and dimensionless due to <math>\int\delta(p^2-m^2)d^4p=1</math>.
Hydrodynamics assumes local equilibrium, which implies that we know how to obtain the expectation value such as <math>\langle |a^+_{p_1}a_{p_1} |\rangle</math> once the system evolution is determined. For a static source, once the particle density <math>n</math> is obtained, one can calculate the particle number by a spatial integral.
- <math>\begin{align}
N=\int n d^3x \end{align}</math>
The above integral can be seen as carried out at constant time, which is not the case when hadrons freeze-out in the final stage of hydrodynamic evolution. From an hydrodynamical point of view, the freeze-out surface is not necessarily time-like, it can be any surface in 4-space. The hadrons measured by the detector only consist of those whose fluxes pass the surface element. Therefore, one has to generalize the above expression to a form which is covariant, namely, a contraction. Following this line of thought, the term <math>d^3x</math> should be understand as an infinitesimal dual vector, in other words, the surface element is a four dual vector which only has time component. Therefore, the particle number is given by the contraction of surface element and particle four momentum.
- <math>\begin{align}
p^0N=\int_{\sigma} d\sigma_{\mu}p^{\mu}f(x,p) \end{align}</math>
Using Wick theorem, one shows that the two-particle correlation can be simplifies to the summation of three terms, all of which only involves two point Green functions.
- <math>\begin{align}
\langle |a^+_{p_1}a^+_{p_2}a_{p_2}a_{p_1}|\rangle = \langle |a^+_{p_1}a_{p_1}|\rangle\langle |a^+_{p_2}a_{p_2}|\rangle +\langle |a^+_{p_1}a_{p_2}|\rangle\langle |a^+_{p_2}a_{p_1}|\rangle +\langle |a^+_{p_1}a^+_{p_2}|\rangle\langle |a_{p_2}a_{p_1}|\rangle \end{align}</math>
The first term is, in fact, the product of one-particle distribution. We have discussed above how to evaluate it in hydrodynamics, however, it is not even necessary in this context, since it is exactly the same form as the denominator, therefore gives a constant of 1. The second term corresponds to HBT effect, and the third term corresponding to back to back correlation. Consider the following pure state
- <math>|\phi\rangle \equiv \mathcal{C}|(a^+_k)^2\rangle+\mathcal{D}|(a^+_k)^3\rangle+\mathcal{E}|(a^+_{k'})^2\rangle+\mathcal{F}|(a^+_{k'})^3\rangle</math>
where <math>\mathcal{C} \mathcal{D}\mathcal{E} \mathcal{F}</math> are normalization constants. It is straightforward to verify that none of the following expectation value vanishes,
- <math>\begin{align}
&\langle\phi|a_k|\phi\rangle \\ &\langle\phi|a^+_{k'}a_k|\phi\rangle \\ &\langle\phi|a_{k'}a_k|\phi\rangle \end{align}</math>
In particular, they are non-vanishing for coherent state <math>|\alpha\rangle</math>, which exibits maximal coherence
- <math>\begin{align}
&|\alpha\rangle =e^{-{|\alpha|^2\over2}}\sum_{n=0}^{\infty}{\alpha^n\over\sqrt{n!}}|n\rangle =e^{-{|\alpha|^2\over2}}e^{\alpha a^+}|0\rangle \\ &a|\alpha\rangle = \alpha |\alpha\rangle \end{align}</math>
The only problem with such coherent state is that they will tend to collapse to an ensemble of energy eigen-states in a thermal environment. Due to the second law of thermodynamics, entropy obtains its maximum when the system is in equilibrium, leading to the canonical distribution, which is known as thermal decoherence (see Sakurai Modern Quantum Mechanics(3.4.48)). The effect of decoherence, in terms of density matrix, is essentially the decay or rapid vanishing of the off-diagonal elements of the partial trace of the joint system's density matrix, i.e. the trace, with respect to any environmental basis, of the density matrix of the combined system and its environment. The decoherence irreversibly converts the "environmentally traced over" density matrix from a pure state to a reduced mixture (see arXiv:quant-ph/0105127). Due to this very reason, the third therm is usually understood to be zero, but we will come back with more details in the below.
- <math>\begin{align}
\langle |a^+_{p_1}a^+_{p_2}|\rangle = 0 \end{align}</math>
Now let us focus on HBT effect. Sinyukov has shown (see arXiv: nucl-th/9909018) that such terms can be written using Wigner function as following
- <math>\begin{align}
&\langle a^+_{p_1}a_{p_2}\rangle =\int d\sigma_{\mu} p^{\mu}e^{iq\cdot x} f_W(x,p) \\ &f_W(x,p) \equiv \int d^4u (2\pi)^{-3}e^{-iu\cdot x}\delta(p\cdot u)\langle a^+(p-\frac{u}{2})a(p+\frac{u}{2})\rangle \end{align}</math>
where <math>f_W(x,p)</math> is the single particle Wigner function. The above expression is general, except it is written in a covariant form as we did for one-particle distribution function. As a result, the l.h.s. which is equal time two-point Green function into the r.h.s. where the integral is carried out on the freeze-out surface (the two-point Green function is still at equal time).
Then it is argued that at the limit when the density matrix is diagonal enough, one can replace the Wigner function with Bose-Einstein distribution for bosons.
- <math>\begin{align}
&f_W(x,p)\to f_{B}(p\beta u) = \frac{(2\pi)^{-3}}{exp(\beta p\cdot u) - 1}\\ &\beta = \frac{1}{T} \end{align}</math>
In hydrodynamics, the most simple scenario for the freeze-out surface is the Cooper-Frye sudden freeze-out at <math>T=T_f=\text{const.}</math>. This freeze-out temperature should be the same as that one uses to study the <math>p_T</math> spectra. We neglect the resonance decays in this work. Since it was argued that, since resonance decays contribute to the correlations with very small <math>q</math> values, the experimentally determined HBT radii are essentially due to the direct pions.
Putting all the pieces together, we obtains the expression of HBT correlation in hydrodynamics
- <math>\begin{align}
R(p_1,p_2) \equiv C_2^{HBT}(q,P)=1+\frac{|I(q,P)|^2}{I(0,p_1)I(0,p_2)} \end{align}</math>
where
- <math>\begin{align}
&I(q,P)\equiv \int_{\sigma=T_f}d\sigma_\mu P^\mu f(x,P)e^{iqx}\\ &P=(p_1+p_2)/2 \\ &q=(p_1-p_2) \end{align}</math>
In SPH representation, we write <math>I(q,P)</math> as
- <math>\begin{align}
I(q,P)=\sum_j \frac{\nu_j n_{j\mu} P^\mu}{s_j |n_{j\mu} u_j^\mu|} {\mathrm{e}}^{iq_\mu x_j^\mu}f(u_{j\mu} P^\mu) \end{align}</math>
where the summation is over all the SPH particles. In the Cooper-Frye freeze-out, these particles should be taken where they cross the hyper-surface <math>T=T_f</math> and <math>n_{j\mu}</math> is the normal to this hyper-surface. Notice that, if we put <math>p_1=p_2=P</math>, so that <math>q=0</math>, <math>I(0,P)</math> is reduced to the inclusive one-particle distribution.
Back to back correlation
As mentioned above, the contribution from the third on the r.h.s. of the Green function gives rise to the so called "Back to back correlation".
- <math>\begin{align}
\langle |a^+_{p_1}a^+_{p_2}a_{p_2}a_{p_1}|\rangle = \langle |a^+_{p_1}a_{p_1}|\rangle\langle |a^+_{p_2}a_{p_2}|\rangle +\langle |a^+_{p_1}a_{p_2}|\rangle\langle |a^+_{p_2}a_{p_1}|\rangle +\langle |a^+_{p_1}a^+_{p_2}|\rangle\langle |a_{p_2}a_{p_1}|\rangle \end{align}</math>
The basic idea was introduced by Asakawa and Csorgo (see arXiv:hep-ph/9612331) that in the ultra-relativistic collisions the hot and dense media may have the hadrons dressed up so that their effective masses are modified, on the other hand, when the hadrons finally go cross the freeze-out surface, they become free particles and are subsequently detected. If one desires to evaluate the ensemble average value of terms such as
- <math>\langle |a_{p_2}a_{p_1}|\rangle = \text{Tr}(\hat{\rho} a_{p_2}a_{p_1})</math>
one should use the density matrix <math>\hat{\rho}</math> of the dressed up hadrons, while <math>a_{p_2}, a_{p_1}</math> are particle creation and annihilation operators in the vacuum. It turns out naturally these terms are non-vanishing in such case. In fact, one can establish two sets of particles creation and annihilation operators, those for the vacuum (<math>a^+_p,a_{p'}</math>) and those for the hot and dense media (<math>b^+_p,b_{p'}</math>), they are connected by the Bogoliubov transformation. The following term serves as an example
- <math>\begin{align}
&\langle |a^+_{p_1}a_{p_2}|\rangle \\ &=\langle |(c_{p_1}^*b_{p_1}^++s_{-p_1}b_{-p_1})(c_{p_2}b_{p_2}+s_{-p_2}^*b_{-p_2}^+)|\rangle\\ &=\langle |c_{p_1}^*c_{p_2}b_{p_1}^+b_{p_2}|\rangle +\langle |c_{p_1}^*s_{-p_2}^*b_{p_1}^+b_{-p_2}^+|\rangle +\langle |s_{-p_1}c_{p_2}b_{-p_1}b_{p_2}|\rangle +\langle |s_{-p_1}s_{-p_2}^*b_{-p_1}b_{-p_2}^+|\rangle\\ &=\langle |c_{p_1}^*c_{p_2}b_{p_1}^+b_{p_2}|\rangle +\langle |s_{-p_1}s_{-p_2}^*b_{-p_1}b_{-p_2}^+|\rangle\\ &=\langle |c_{p_1}^*c_{p_2}b_{p_1}^+b_{p_2}|\rangle +\langle |s_{-p_1}s_{-p_2}^*(b_{-p_2}^+b_{-p_1}+1)|\rangle\\ &=c_{p_1}^*c_{p_2}\langle |b_{p_1}^+b_{p_2}|\rangle +s_{-p_1}s_{-p_2}^*\left(\langle |b_{-p_2}^+b_{-p_1}|\rangle+1\right)\\ \end{align}</math>
However, their calculation only treats homogeneous system, the model Hamiltonian does not contain any coordinate dependent term souce term which describes the spatial distribution of the system in question. As a results, the correlation is non-trivial only at parallel and anti-parallel directions, namely
- <math>\begin{align}
&C_2^{HBT}(p,p')=2\delta(p-p')\\ &C_2^{BBC}(p,p')=\delta(p+p')\left(1+\frac{|s_pc_p^*n_p+s_{-p}c_{-p}^*(n_{-p}+1)|^2}{n_1(p)n_1(-p)}\right) \end{align}</math>
where
- <math>\begin{align}
&c_p = \cosh(r_p)\\ &s_p = \sinh(r_p)\\ &r_p =\frac{1}{2}\log\left[\frac{\omega_p}{\Omega_p}\right]\\ &\omega_p = \sqrt{m^2+{\vec p}^2}\\ &\Omega_p= \sqrt{m_*^2+{\vec p}^2}\\ &n_p=[\exp(\Omega_p/T -1)]^{-1}\\ &n_1(p)=|c_p|^2n_p+|s_k|^2(n_{-p}+1) \end{align}</math>
and <math>m_*</math> is the modified mass.
However, as it is well known, in real collisions, hadrons are emitted from freeze-out surface due to the hydrodynamical nature of the system, and the size of the fireball is finite and the system is far from homogeneous. As pointed out by Gastão and Sandra, such finite volume effect can be effectively taken care of by the Wigner function procedure introduced by Sinyukov. The trick to do this is to try to express the correlation in term of creation and annihilation operator pairs of the hot media in a form similar to that in HBT correlation, namely, <math>\langle|b^+_pb_{p'}|\rangle</math>, then applies Sinyukov's procedure to rewrite it as an integral on the freeze-out surface. Meanwhile one also need to rewrite the remaining coefficients in a covariant fashion. The resulting expressions in terms of <math>\langle|b^+_pb_{p'}|\rangle</math> are
- <math>\begin{align}
&R(p_1,p_2)\equiv C_2(p_1,p_2) =1+\frac{|G_c(p_1,p_2)|^2}{G_c(p_1,p_1)G_c(p_2,p_2)}+\frac{|G_s(p_1,p_2)|^2}{G_c(p_1,p_1)G_c(p_2,p_2)}\\ &G_c(p_1,p_2)=\sqrt{\omega_{p_1}\omega_{p_2}}\left[c_{p_1}^*c_{p_2}\langle |b_{p_1}^+b_{p_2}|\rangle+s_{-p_1}s_{-p_2}^*(\langle |b_{-p_2}^+b_{-p_1}|\rangle+1)\right] \\ &G_s(p_1,p_2)=\sqrt{\omega_{p_1}\omega_{p_2}}\left[s_{-p_1}^*c_{p_2}\langle |b_{-p_1}^+b_{p_2}|\rangle+c_{p_1}s_{-p_2}^*(\langle |b_{-p_2}^+b_{p_1}|\rangle+1)\right] \end{align}</math>
From which, one obtains the expressions which can be used in hydrodynamics (see arXiv:nucl-th/9810034 for details.)
- <math>\begin{align}
&G_c(1,2) \equiv G_c(p_1,p_2)=\frac{1}{(2\pi)^3}\int_{\sigma}d\sigma_{\mu}P_{1,2}^{\mu}e^{iq_{1,2}\cdot x} \left[|c_{1,2}|^2n_{1,2}+|s_{-1,-2}|^2(n_{-1,-2)}+1)\right] \\ &G_s(1,2) \equiv G_s(p_1,p_2)=\frac{1}{(2\pi)^3}\int_{\sigma}d\sigma_{\mu}P_{1,2}^{\mu}e^{2iP_{1,2}\cdot x} \left[s_{-1,2}^*c_{2,-1}n_{-1,2}+c_{1,-2}s_{-2,1)}^*(n_{1,-2}+1)\right] \end{align}</math>
where
- <math>\begin{align}
&P_{i,j}=(p_i+p_j)/2 \\ &q_{i,j}=(p_i-p_j)\\ &\omega_i=p_i \cdot u\\ &\tilde{p}_i= p_i - \omega_i u \\ &\Omega_i=\sqrt{m_*^2-\tilde{p}_i \cdot \tilde{p}_i}\\ &p_i^*=\Omega_i u+ \tilde{p_i}\\ &P^*_{i,j}=(p_1^*+p_2^*)/2\\ \end{align}</math>
where <math>i=1,2</math>, <math>u</math> is the four-velocity of the fluid on the freeze-out surface, <math>\tilde{p}</math> measures the part of the four-momentum orthogonal to the four-velocity, for further discussion, one may also define
- <math>\begin{align}
&p_{\pm i}=\omega u\pm \tilde{p}_{i}\\ &p_{\pm i}^*=\Omega u\pm \tilde{p}_{i} \end{align}</math>
where <math>p_{-1}, p_{-2}</math> are the momenta which inverts the parts of <math>p_1, p_2</math> orthogonal to the fluid four-velocity, and from this moment on, all these momenta will be denoted by <math>p_i</math> while bearing in mind that <math>i=\pm 1, \pm 2</math>. Based on the above definiations, we further define the following quantities,
- <math>\begin{align}
&c_{i,j} = \cosh\left[r(i,j)\right]\\ &s_{i,j} = \sinh\left[r(i,j)\right]\\ &r(i,j) =\frac{1}{2}\log\left[\frac{P_{i,j} \cdot u}{P^*_{i,j}\cdot u}\right]\\ &n_{i,j} =[\exp((P^*_{i,j}\cdot u)/T -1)]^{-1} \end{align}</math>
where we have adopted the same definition as before
- <math>\begin{align}
&P_{i,j}=(p_i+p_j)/2 \\ &P^*_{i,j}=(p^*_i+p^*_j)/2 \end{align}</math>
It is worth noting, as pointed out by Gastão, the reason $2P_{i,j}$ appears on the exponential of <math>G_s</math> in stead of $q_{i,j}$ is that one has to carry out the Bogoliubov transformation before applying Sinyukov's formulae for curved freeze-out surface. The reason is following. If one applies Sinyukov's formulae first, one still obtains an expression involving a Wigner function, except the two momenta in the ensemble average are very different that one cannot approximate them by the equilibrium distribution.
Here I am not sure what was the purpose to introduce symbols such like <math>c_{i,j}, n_{i,j}</math>, since they only depend on the component of average momentum <math>P_{i,j}</math> parallel to the fluid four-velocity, which came as a natural generalization of Sinyukov's formulae. One simply has
- <math>\begin{align}
&c_{i,j} = c_{|i|,|j|}\\ &s_{i,j} = s_{|i|,|j|}\\ &r(i,j) =r_{|i|,|j|}\\ &n_{i,j} =n_{|i|,|j|} \end{align}</math>
The last step is to write everything in terms of SPheRIO variables, which reads
- <math>\begin{align}
&G_c(1,2) \equiv G_c(p_1,p_2)=\frac{1}{(2\pi)^3}\sum_j \frac{\nu_j n_{j\mu} P_{1,2}^\mu}{s_j |n_{j\mu} u_j^\mu|}e^{iq_{1,2}\cdot x} \left[|c_{1,2}|^2n_{1,2}+|s_{-1,-2}|^2(n_{-1,-2}+1)\right] \\ &G_s(1,2) \equiv G_s(p_1,p_2)=\frac{1}{(2\pi)^3}\sum_j \frac{\nu_j n_{j\mu} P_{1,2}^\mu}{s_j |n_{j\mu} u_j^\mu|}e^{2iP_{1,2}\cdot x} \left[s_{-1,2}^*c_{2,-1}n_{-1,2}+c_{1,-2}s_{-2,1}^*(n_{1,-2}+1)\right] \end{align}</math>
Particle and anti-particle
The above results hold only for particles that are their own antiparticles, e.g. the <math>\phi</math> meson and <math>\pi^0</math>. In a general case, the Bogoliubov transformation will mix particles with antiparticles, but the extension to particle-antiparticle correlations is quite straightforward. For instance, the particle-antiparticle involves the evaluation of the following term
- <math>\begin{align}
&\langle |a^+_{p_1}\bar{a}_{p_2}|\rangle \\ &=\langle |(c_{p_1}^*b_{p_1}^++s_{-p_1}\bar{b}_{-p_1})(c_{p_2}\bar{b}_{p_2}+s_{-p_2}^*b_{-p_2}^+)|\rangle\\ &=\langle |c_{p_1}^*c_{p_2}b_{p_1}^+\bar{b}_{p_2}|\rangle +\langle |c_{p_1}^*s_{-p_2}^*b_{p_1}^+b_{-p_2}^+|\rangle +\langle |s_{-p_1}c_{p_2}\bar{b}_{-p_1}\bar{b}_{p_2}|\rangle +\langle |s_{-p_1}s_{-p_2}^*\bar{b}_{-p_1}b_{-p_2}^+|\rangle\\ &=\langle |c_{p_1}^*c_{p_2}b_{p_1}^+\bar{b}_{p_2}|\rangle +\langle |s_{-p_1}s_{-p_2}^*\bar{b}_{-p_1}b_{-p_2}^+|\rangle\\ &=\langle |c_{p_1}^*c_{p_2}b_{p_1}^+\bar{b}_{p_2}|\rangle +\langle |s_{-p_1}s_{-p_2}^*(b_{-p_2}^+\bar{b}_{-p_1}+1)|\rangle\\ &=c_{p_1}^*c_{p_2}\langle |b_{p_1}^+\bar{b}_{p_2}|\rangle +s_{-p_1}s_{-p_2}^*\left(\langle |b_{-p_2}^+\bar{b}_{-p_1}|\rangle+1\right)\\ &=0 \end{align}</math>
which was non-vanishing in the previous case. As a result, the identical particle correlation does not have the contribution from <math>G_s</math>, while the particle-antiparticle correlation does not receive contribution from <math>G_c</math>. Besides, one need to take bit more care to identify the particle and substitute correct chemical potential when applying integral on the freeze-out surface. Other than that, things remain unchanged, since they have the same mass, and the formulae do not involve charges.
Implementation in SPheRIO
Momentum space
The momentum space defined by <math>\vec p_1</math> and <math>\vec p_2</math> is of 6 dimensions. In the first place, we choose the following two dimensional subspace to present our result. Since we wish to show HBT and back-to-back correlations, we will only pick particle pairs with <math>\zeta,\pm\zeta</math> in pseudo-rapidity to make sure the pair is always in the parallel or anti-parallel directions, the value of <math>\zeta</math> is then randomly drawn by a Monte Carlo generator. Next, we will only select those particle pairs whose transverse momenta is <math>p_T</math> are alone the x-axis. Similar to the HBT implementation in SPheRIO, the event can be rotated by select random reaction plane in NEXUS. Now, only two free parameters left, namely, the magnitude of the two transverse momentum. The resulting momenta of the particle pair are
- <math>\vec p_1 = \{p_{1T},0,p_{1T}\sinh(\zeta)\} </math>
- <math>\vec p_2 = \{-p_{2T},0,p_{2T}\sinh(-\zeta)\} </math>
with <math>0<p_{1T}<+\infty</math> and <math>-\infty<p_{2T}<+\infty</math>.
Modified mass
We use the ansatz proposed in the Gyulassy's paper.
- <math>m_*= m\left[1+\exp(-|\vec p|^2/\Lambda^2)\right]</math>
Asymptotic behaviour
When <math>m_* \to m</math>, one gets <math>G_s \to 0</math> and <math>G_c \to G_{HBT}</math>. This can be used to numerically check the implementation.
Numerical results
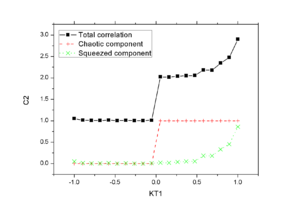
Fig.1 shows the correlations with <math>m^*=2m</math> for <math>\pi^0</math>.
The asymptotic behaviour of HBT correlation is as expected, it goes to 2 at <math>k_1=k_2</math> and it vanishes when <math>k_1=-k_2</math>. However, the asymptotic behaviour of BBC correlation is very different from what was discussed in Gyulassy's PRL paper, it does not increase at <math>k_1=-k_2 \to \infty</math>, instead it increases at <math>k_1=k_2</math>.
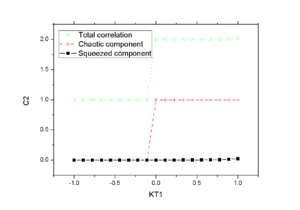
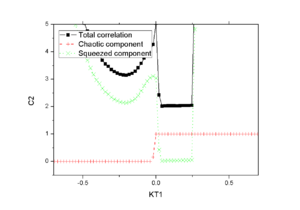
Such asymptotic hehaviour still presents but with a much smaller magnitude when one uses an effective mass close to the orginal value, as one can see in Fig.2a and Fig.2b. These results are consistent with the mass scan plot shown below.
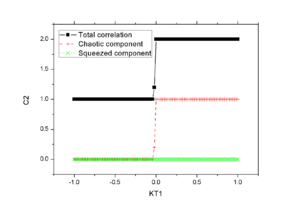
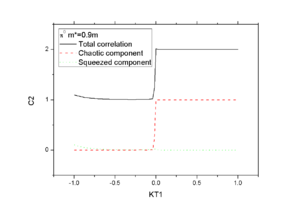
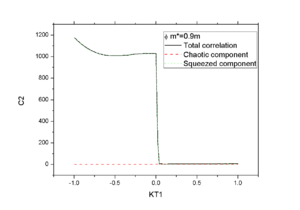
When the smaller mass <math>m^*=0.9m</math> is used, one note that it generates a quite reasonable result.
As a side note, the following relations hold when the freeze-out surface integral is smooth enough,
- <math>\int d\sigma_\mu P^\mu e^{iq\cdot x} \to \delta(\vec{q})</math>
- <math>\int d\sigma_\mu P^\mu e^{2iP\cdot x} \nrightarrow \delta(p_1^0+p_2^0)\delta(\vec{P}) \to 0</math>
In the second expression, we do not have a factor of <math>\delta</math> function, as Gastão pointed out. For instance <math>d\sigma_\mu \to t^2-\vec{x}^2=\tau^2=const.</math>
- <math>\int d\sigma_\mu P^\mu e^{2iP\cdot x} \sim \delta\left(\sqrt{{P^0}^2-\vec{P}^2}\right) </math>
which can be obtained straightforwardly by considering first the case when <math>P^0=0</math>, then the expression in general must be invariant. Following this line of thought, we found that BBC goes to zero when <math>P^0>0</math>.
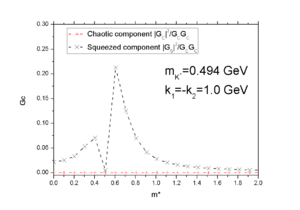
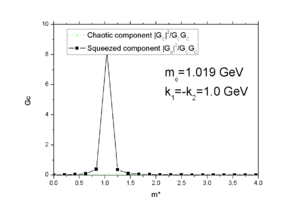
As suggested by Sandra, in Fig.3-5, we show the mass dependence of the correlation, at back-to-back direction with <math>k_1=-k_2=1.0GeV</math>, one sees that the correlation hits zero at <math>m^*=m_{\pi}</math> as expected, but the magnitude at other points is very small. The four plots are from two different events with different precision, the two plots at the top-right and top-left corner are done with a resolution of 50*100, they are of the same data but showing different range; the two plots at bottom-right and bottom-left corner are from another random event with a resolution of 100*200. It seems that these results are consistent.
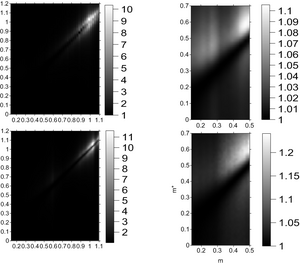
From a more general perspective, Fig.6 presents the result of a mass scan, <math>C_2</math> is calculated as a function of <math>m</math> and <math>m^*</math>, the black strip of <math>C_2=1</math> at <math>m=m^*</math> is expected. One sees when the mass is big enough, the correlation goes to as big as <math>1.5</math>. We note that the results here are in consistence with the observations, namely, BBC was not observed for <math>\pi^0</math>, which corresponds to the dark region <math>m\sim m^* \sim 0.15 GeV</math> with negligible <math>C_2</math>.
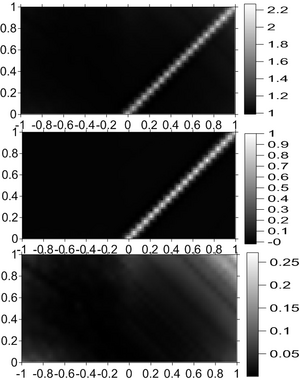
In Fig.7-8 we show the momentum scan of particle correlation of <math>\pi^0</math>. One sees that in this case, BBC has non-trivial feature at <math>k_1=k_2</math> where HBT gives strictly a constant of 2.
Different Scenarios
Now we present results of two different scenarios according to the discussions on 04/22/2013. The second scenario reads
- <math>\begin{align}
&G_c(1,2) \equiv G_c(p_1,p_2)=\frac{1}{(2\pi)^3}\sum_j \frac{\nu_j n_{j\mu} P_{1,2}^\mu}{s_j |n_{j\mu} u_j^\mu|}e^{iq_{1,2}\cdot x} \left[|c_{1,2}|^2n_{1,2}+|s_{-1,-2}|^2(n_{-1,-2}+1)\right] \\ &G_s(1,2) \equiv G_s(p_1,p_2)=\frac{1}{(2\pi)^3}\sum_j \frac{\nu_j n_{j\mu} P_{1,2}^\mu}{s_j |n_{j\mu} u_j^\mu|}e^{i\tilde{q}_{1,2}\cdot x} \left[s_{-1,2}^*c_{2,-1}n_{-1,2}+c_{1,-2}s_{-2,1}^*(n_{1,-2}+1)\right] \end{align}</math>
The third scenario reads
- <math>\begin{align}
&G_c(1,2) \equiv G_c(p_1,p_2)=\frac{1}{(2\pi)^3}\sum_j \frac{\nu_j n_{j\mu} P_{1,2}^\mu}{s_j |n_{j\mu} u_j^\mu|}e^{iq_{1,2}\cdot x} \left[|c_{1,2}|^2n_{1,2}+|s_{-1,-2}|^2(n_{-1,-2}+1)\right] \\ &G_s(1,2) \equiv G_s(p_1,p_2)=\frac{1}{(2\pi)^3}\sum_j \frac{\nu_j n_{j\mu} \tilde{P}_{1,2}^\mu}{s_j |n_{j\mu} u_j^\mu|}e^{i\tilde{q}_{1,2}\cdot x} \left[s_{-1,2}^*c_{2,-1}n_{-1,2}+c_{1,-2}s_{-2,1}^*(n_{1,-2}+1)\right] \end{align}</math>
where
- <math>\tilde{q}\equiv (q^0,\vec{P})</math>
- <math>\tilde{P}\equiv (P^0,\vec{q})</math>
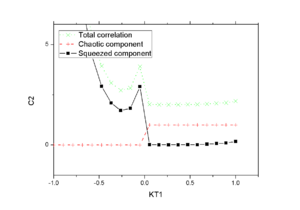
The resulting correlation of the second scenario for <math>\pi^0</math> is shown in Fig.9a. We note that the only modification comes from the BBC part, and it gives the correct hehaviour described in the literature.
In Fig.9.b-d, we show the same plot but with <math>m^*=0.9m</math> for <math>\pi^0, K^+, \phi</math>.
The corresponding results of the third scenario is shown in Fig.10. Though it give correct behaviour at back-to-back direction, the BBC correlation does not converge at parallel direction.
Now one may argue at this moment that the formulae for BBC is not valid at parallel direction, since the approximation <math>\vec{k}_1=-\vec{k}_2</math> one adopts for the Wigner function is not satisfied at those region. Similar arguments may be used for similar situations.
To be updated.